*-9+63 Schkval-Torpedo

The Russian Shkval-Torpedo

Pictures of the russian Shkval-torpedo in the web (see: Shkval at Wikipedia) present a mainly cylindrical body with a long ellipsoidal head bearing a flat circular plate.

The data presented by Wikipedia:

   length     :          8.2   m
   diameter :        533   mm
   mass       :      2700   kg
   velocity :        350   km/h

The following calculation assumes some estimated data:

diameter of plate:
200 mm

length of ellipsoidal part:
2.6 m

length of cylinder:
5.5 m

Calculation of density

The estimated data deliver a volume of ca. 1.6 m³ and a density of ca. 1.69 g/cm³.

Assuming a water density of 1.027 g/cm³ the torpedo would have a negative buoyancy of 66%. (Compared to torpedos of world war II which had a negative buoyancy of ca. 20%).

Calculation of cavitation bubble at velocity of 350 km/h (ca. 100 m/s)

According to equation (see Cavitation Laws)

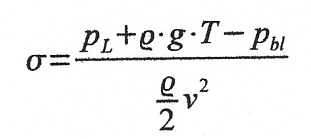
the cavitation number for bubble pressure 0 bar und a depth of 10 m equals 0.042.
The table shows besides the cavitation number also the correspondent data bubble diameter and length for different depths:

depth 15 m 10 m 6 m 5 m
σ 0.052 0.042 0.034 0.032
bubble diameter 0.8 m 0.89 m 0.99 m 1.02 m
bubble length 6.4 m 8.17 m 10.4 m 10.94 m

In depths of 10 m respectively 15 m the length of the generated cavitation bubble is too small to guarantee supercavitating running. In a depth of 6 m the dimensions of the bubble are large enough to envelop the whole torpedo without touching the water.
The limitation of depth within a small region around 6 m facilitates the defense of supercavitating rockets.

Stationary running in depth of 6 m .

Wikipedia writes: "The missile controls its direction using four fins that skim the inner surface of the supercavitation envelope. To change direction, the fin or fins on the inside of the desired turn are extended, and the opposing fins are retracted. To make faster turns the push plate on the nose can be used to control the shape of the bubble the missile is traveling in."
Regarding the dimensions of the fins it seems impossible to use them for moving the missile in the bubble. Another explanation seems more plausible.The fins could be regarded as sensors to measure the dimension of the bubble near the rear of the missile. If the fins show big distance to the wall of the bubble the push plat at the nose is inclined so that a force is induced which moves the nose in greater depth where the cavitation bubble becomes smaller following the Reichardt Laws of Cavitation Bubbles. If the fins show small distance to the wall the push plate is inclined in the opposite direction and the missile gets in lower depth where the bubble becomes larger so that supercavitating running is ensured. Thereby running in constant depth is guaranteed.

Rocket thrust during stationary supercavitating running

Using the assumed data to calculate the necessary rocket thrust delivers ca. 130 kN .
May be this thrust is realized by increasing the mass flow of the rocket by injecting water in the rocket nozzle. This could be an explanation for the broad opening in the missile nose (ca. 7 cm). If this opening should only be for measuring the dynamic pressure the opening could be much smaller.

Launching the Shkval from plunged submarine

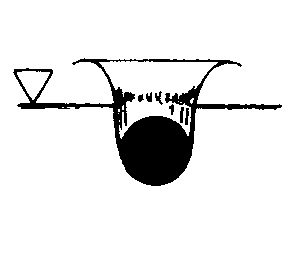
Trusting the information in the web the Shkval is launched from a conventional torpedo tube in depth up to 100 m with a velocity of ca. 25 m/s. Under these conditions it is necessary to generate artificial gas pressure around the missile in order to realize supercavitating running. By means of 3 bell-shaped caps (see figure above) beneath the push plate apparently gas is pouring out of a gas generator.

After launch of the missile apparently the 8 auxiliary small rockets are ignited to guarantee a security distance to the submarine before ignition of the main rocket engine which accelerates the missile to a velocity, where supercavitating running is guaranteed without artificial gas generation.

home back more